5 描述性统计分析

5.1 若干概念

1. 随机变量

当一件事情的结果无法预料时，就叫随机现象。表示随机现象一组结果的变量就是随机变量。

比如说，调查了100 个人的身高，这100 个身高的数据是随机变量身高的数据。并不是说这些身高值是不固定可变的，而是这100 个身高值是一次调查的结果，再调查100 个人就是另一组不同的100 个身高值。

2. 概率分布

随机变量既然是这样随机的，还有必要研究它吗？有必要！因为把多个随机结果放在一起的时候，能发现一定的规律性。比如100 人的身高可能对称地分布在175cm 附近，离得越远人数越少，即表现出一种正态分布规律性。随机现象五花八门，但每一种随机现象表现出来的规律性是固定的，用数学语言表达出来就是概率分布。所以，不同概率分布就是不同随机现象规律性的数学描述。

统计学最常用到四大概率分布：正态分布、t 分布、卡方分布、F 分布。

比如正态分布 $𝑁 (𝜇, 𝜎^{2})$ , 𝜇 和𝜎 （小写的sigma）就是参数，它们只要取不同值，就是不同的分布形状。

3. 总体和样本

总体(population)：是包含所研究的全部个体（数据）的集合。
样本(sample)：从总体中抽取的一部分个体的集合，样本包含个体的数目称为样本量。

抽样的目的是根据样本数据提供的信息推断总体的特征，或者说，用样本统计量推断总体参数。

比如，要研究天津市成年男性的身高，则所有天津市成年男性的身高数据就是总体，但实际上不可能把所有这些身高都测量一遍，只能是随机抽取一部分，比如100 人，测得身高数据，这就是样本，样本量是100。

4. 参数与统计量

参数(parameter)：用来描述总体特征的概括性值，是研究者想要了解的总体的某种特征值，如总体均值(𝜇)、总体方差(𝜎2)、总体比例(𝜋) 等

统计量(statistic)：是用来描述样本特征的概括性数字度量，是根据样本数据计算出来的量，由于抽样是随机的，因此统计量是样本的函数。与上面总体参数对应的统计量是样本均值 (𝑥)̄ 、样本标准差 (𝑠2)、样本比例 (𝑝) 等。

由于总体数据通常是不知道的，故参数是未知常数。所以才进行抽样，根据样本计算出相应统计量值去估计总体参数值。

5.2 （样本）统计量

5.2.1 数据位置的统计量

1. 均值(Mean)

均值，度量数据分布的中心位置：

$\bar{x} = \frac{1}{n} \sum_{i = 1}^{n} x_{i}$

2. 中位数(Median)

中位数，是位于最中间的那个数据，比中位数大和小的数据各占观测值的一半。先将数据从小到大排序为： $x_{(1)}$ , ⋯ , $x_{(𝑛)}$ ，然后计算

$x_{0.5} = {\begin{cases} x_{(\frac{n + 1}{2})} & n 为奇数 \\ \frac{1}{2} (x_{(\frac{n}{2})} + x_{(\frac{n}{2} + 1)}) & n 为偶数 \end{cases}$

中位数的优点是具有稳健性，即不受个别极端数据的影响。一般来说，正态分布的数据用均值描述，偏态分布的数据最好是用中位数描述。比如，人均工资有被平均了的感觉，中位数工资才是更合适的中间收入。

3. 分位数(Quantile)

中位数是0.5 分位数，位于0.5 位置的数。

0.25 分位数，称为下四分位数(Q1), 是位于0.25 那个位置的数，即比它小的数占比是0.25, 比它大的数占比是0.75。 0.75 分位数，称为上四分位数(Q3)。

更一般地， $𝑝$ 分位数，是位于 $𝑝$ 位置的数，即比它小的数占比是 $𝑝$ , 比它大的数占比是 $1 - 𝑝$ . 或者说 $𝑛 𝑝$ 的数比它小， $𝑛 (1 - 𝑝)$ 的数比它大。

4. 众数(Mode)

众数，是观测值中出现次数最多的数，对应分布的最高峰。众数常用于分类数据，即出现频数最高的值。

5.2.2 数据分散程度的统计量

极差(Range)

极差，就是数据中的最大值和最小值之差

四分位距(Interquartile Range)

四分位距，是上下四分位数之差，即

$𝐼 𝑄 𝑅 = 𝑄 3 - 𝑄 1$ 样本方差(Variance)

$s^{2} = \frac{1}{n - 1} \sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}$

注意，分母除的是 $𝑛 - 1$ , 这是为了保证用样本方差估计总体方差时，得到的是无偏估计。

这个 $𝑛 - 1$ 也是自由度，在统计学中，几乎所有方法、所有统计量都会涉及自由度。自由度，是计算样本统计量时能够自由取值的数值的个数。

总体方差公式（除以 $𝑛$ ）时，是 $𝑛$ 个样本自由地从总体里抽取。但是样本方差公式时多了一个约束条件，它们的和除以 $𝑛$ 必须等于样本均值 $\bar{x}$ ，所以自由度 𝑛 减去1 个约束条件对自由度的损失，等于 $𝑛 - 1$ 。

不同统计方法的自由度都不一样，但基本原则是每估计1 个参数，就需要消耗 1 个自由度。

以回归分析为例，若有𝑚 个自变量，则需要估计𝑚 + 1 个参数（包含截距项），所以模型的F 检验用到的自由度是𝑛 − (𝑚 + 1). 这意味着只剩下 𝑛 − (𝑚 + 1) 个可以自由取值的数值用来估计模型误差

样本标准差(Standard Deviation) 样本方差的平方根即为标准差𝑠. 标准差的量纲与原数据一致。

变异系数(Coefficient of Variation) 变异系数，是将标准差占均值的百分比，可用于比较不同量纲数据的分散性：

$c_{v} = \frac{s}{\bar{x}} \times 100 %$

5.2.3 样本统计量的R实现

mean(x): 计算数值向量x 的均值
median(x): 计算数值向量x 的中位数
quantile(x, p): 计算数值向量x 的p 分位数
rstatix::get_mode(x): 计算向量x 的众数
max(x)-min(x): 计算数值向量x 的极差
IQR(x): 计算数值向量x 的四分位距
var(x): 计算数值向量x 的样本方差
sd(x): 计算数值向量x 的样本标准差
100*sd(x)/mean(x): 计算数值向量x 的变异系数

很多包提供了同时对多个变量进行（分组）描述汇总所有常见统计量的函数，其中tidy 风格的是rstatix::get_summary_stats() 和 dlookr::describe().

library(rstatix)
iris %>%
  group_by(Species) %>%
  get_summary_stats(type = "full")

## # A tibble: 12 × 14
##    Species variable     n   min   max median    q1    q3   iqr   mad  mean    sd
##    <fct>   <fct>    <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
##  1 setosa  Sepal.L…    50   4.3   5.8   5     4.8   5.2  0.4   0.297 5.01  0.352
##  2 setosa  Sepal.W…    50   2.3   4.4   3.4   3.2   3.68 0.475 0.371 3.43  0.379
##  3 setosa  Petal.L…    50   1     1.9   1.5   1.4   1.58 0.175 0.148 1.46  0.174
##  4 setosa  Petal.W…    50   0.1   0.6   0.2   0.2   0.3  0.1   0     0.246 0.105
##  5 versic… Sepal.L…    50   4.9   7     5.9   5.6   6.3  0.7   0.519 5.94  0.516
##  6 versic… Sepal.W…    50   2     3.4   2.8   2.52  3    0.475 0.297 2.77  0.314
##  7 versic… Petal.L…    50   3     5.1   4.35  4     4.6  0.6   0.519 4.26  0.47 
##  8 versic… Petal.W…    50   1     1.8   1.3   1.2   1.5  0.3   0.222 1.33  0.198
##  9 virgin… Sepal.L…    50   4.9   7.9   6.5   6.22  6.9  0.675 0.593 6.59  0.636
## 10 virgin… Sepal.W…    50   2.2   3.8   3     2.8   3.18 0.375 0.297 2.97  0.322
## 11 virgin… Petal.L…    50   4.5   6.9   5.55  5.1   5.88 0.775 0.667 5.55  0.552
## 12 virgin… Petal.W…    50   1.4   2.5   2     1.8   2.3  0.5   0.297 2.03  0.275
## # ℹ 2 more variables: se <dbl>, ci <dbl>

5.3 统计图

描述统计是从不同方面对数据做了概要，想要进一步了解和探索数据，离不开绘制统计图。不同类型的数据，适用不同类型的统计图。

5.3.1 分类数据的统计图

1. 条形图(Histogram)

条形图是最常用的类别比较图，是用竖直（或水平）的条形展示分类变量的分布（频数），条形的高度代表频数。

geom_bar(): 对原始数据绘制条形图
geom_col(): 对汇总频数/频率的数据用绘制条形图

以starwars 数据集skin_color 绘制条形图为例：

用fct_lump() 将频数≤ 5 的类别做了合并
分组汇总，计算各组频数和频率
绘制条形图，将分类变量skin_color 按频率做了因子重排序，实现了对” 条形” 排序
在条形旁边增加文字注释，标记该条形所占百分比
翻转坐标轴，变成水平条形图

df <- starwars %>%
  mutate(skin_color = fct_lump(skin_color, n = 5)) %>%
  count(skin_color, sort = T) %>%
  mutate(p = n / sum(n))
df

## # A tibble: 6 × 3
##   skin_color     n      p
##   <fct>      <int>  <dbl>
## 1 Other         41 0.471 
## 2 fair          17 0.195 
## 3 light         11 0.126 
## 4 dark           6 0.0690
## 5 green          6 0.0690
## 6 grey           6 0.0690

ggplot(df, aes(fct_reorder(skin_color, p), p)) +
  geom_col(fill = "steelblue") + # 汇总数据制作条形图
  scale_y_continuous(labels = scales::percent) + ## 坐标轴标签由小数变成百分比形式
  labs(x = "皮肤颜色", y = "占比") +
  geom_text(aes(
    y = p + 0.04, ## y的偏移量
    label = str_c(round(p * 100, 1), "%")
  ), ## 将多个字符串合并成一个字符串
  size = 5, color = "red"
  ) +
  coord_flip() ## 翻转xy坐标轴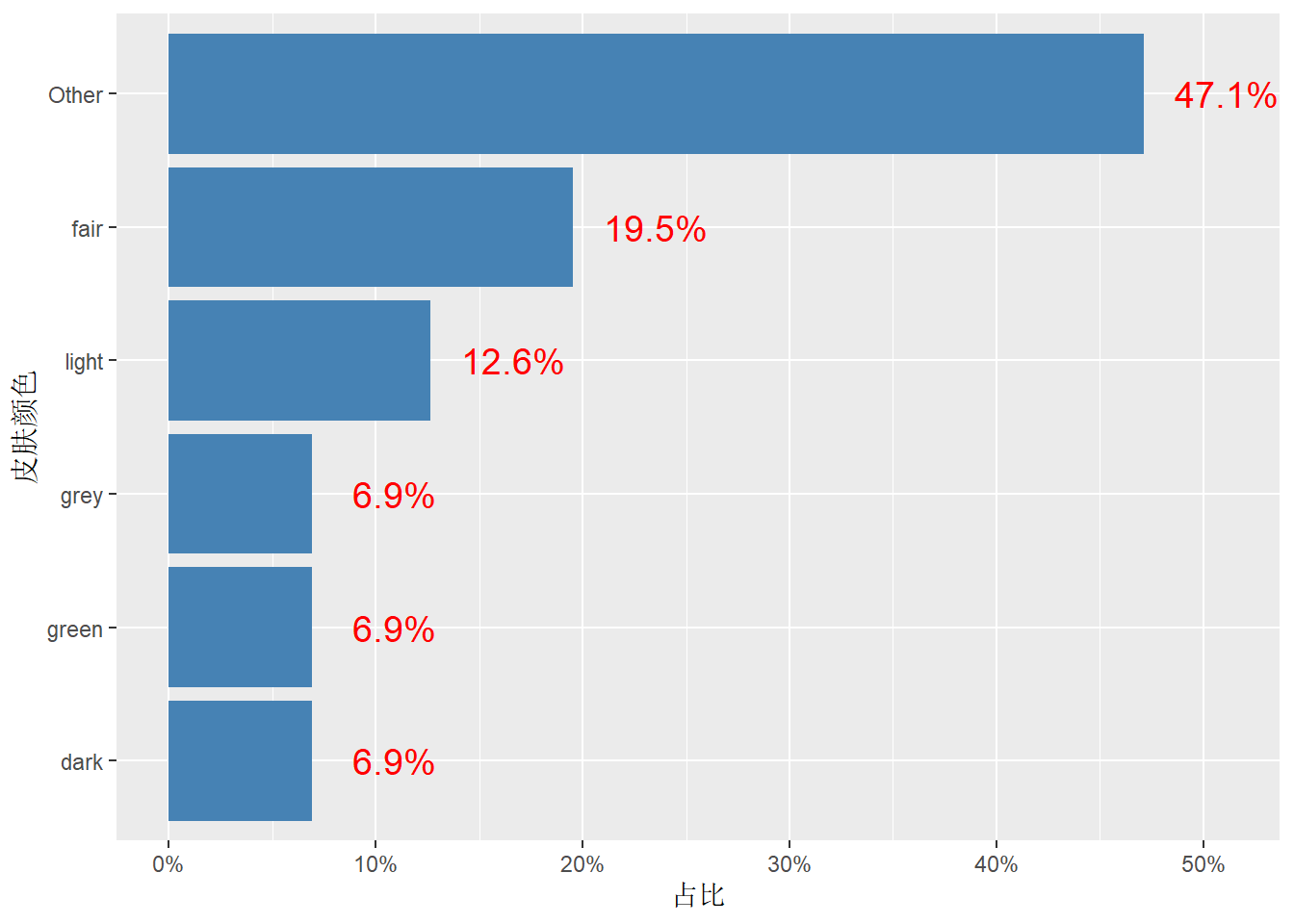

2. 饼图

待补充

5.3.2 连续数据的统计图

1. 直方图

连续数据常用直方图来展示变量取值的分布，利用直方图可以估计总体的概率密度。将变量取值的范围分成若干区间。直方图是用面积而不是用高度来表示数，总面积是100%. 每个区间矩形的面积恰是落在该区间内的百分数（频率），所以

矩形的高= 频率/区间长度= 密度

特别地，若区间是等长的，则” 矩形的高” 就是频率。注意：直方图矩形之间是没有间隔的。

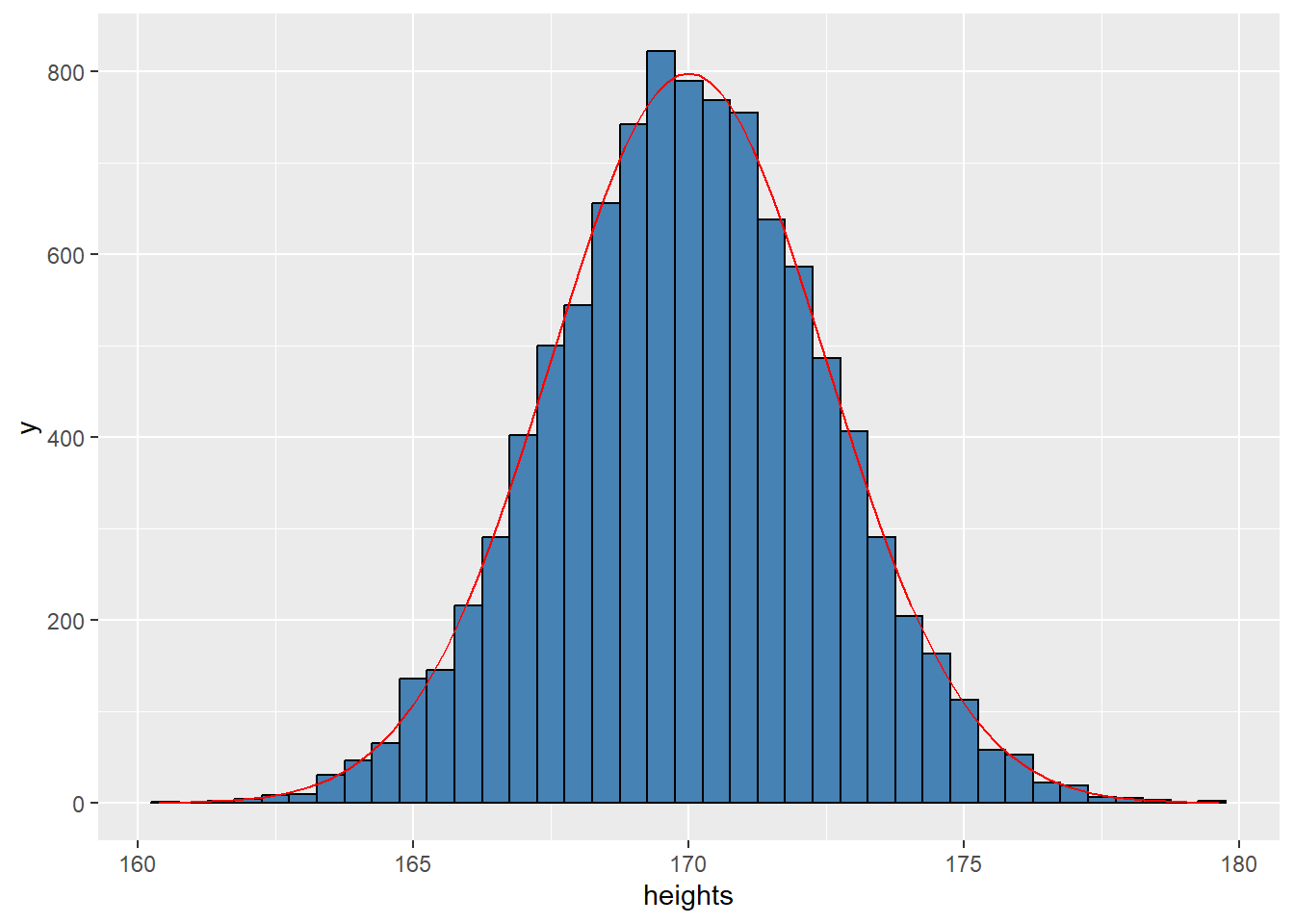
用geom_histogram() 绘制直方图。频率直方图与概率密度曲线正好搭配，因为频率直方图的条形宽度趋于0，就是概率密度曲线。

若想绘制频数直方图+ 概率密度曲线，就需要对密度做一个放大：条形宽度 * 样本数倍。

set.seed(123)
df <- tibble(heights = rnorm(10000, 170, 2.5))
ggplot(df, aes(x = heights)) +
  geom_histogram(
    fill = "steelblue", color = "black",
    binwidth = 0.5
  ) +
  stat_function(
    fun = ~ dnorm(.x, mean = 170, sd = 2.5) * 0.5 * 10000,
    color = "red"
  )

2. 箱线图

箱线图，是在一条数轴上：

以数据的上下四分位数(Q1-Q3) 为界画一个矩形盒子（中间50% 的数据落在盒内）；
在数据的中位数位置画一条线段为中位线；
默认延长线为盒长的1.5 倍，之外的点认为是异常值。

箱线图的主要应用就是，剔除数据的异常值、判断数据的偏态和尾重、可视化组间差异。

用geom_boxplot() 绘制箱线图，例如比较不同drv 下，hwy 的组间差异

ggplot(mpg, aes(x = drv, y = hwy)) +
  geom_boxplot()

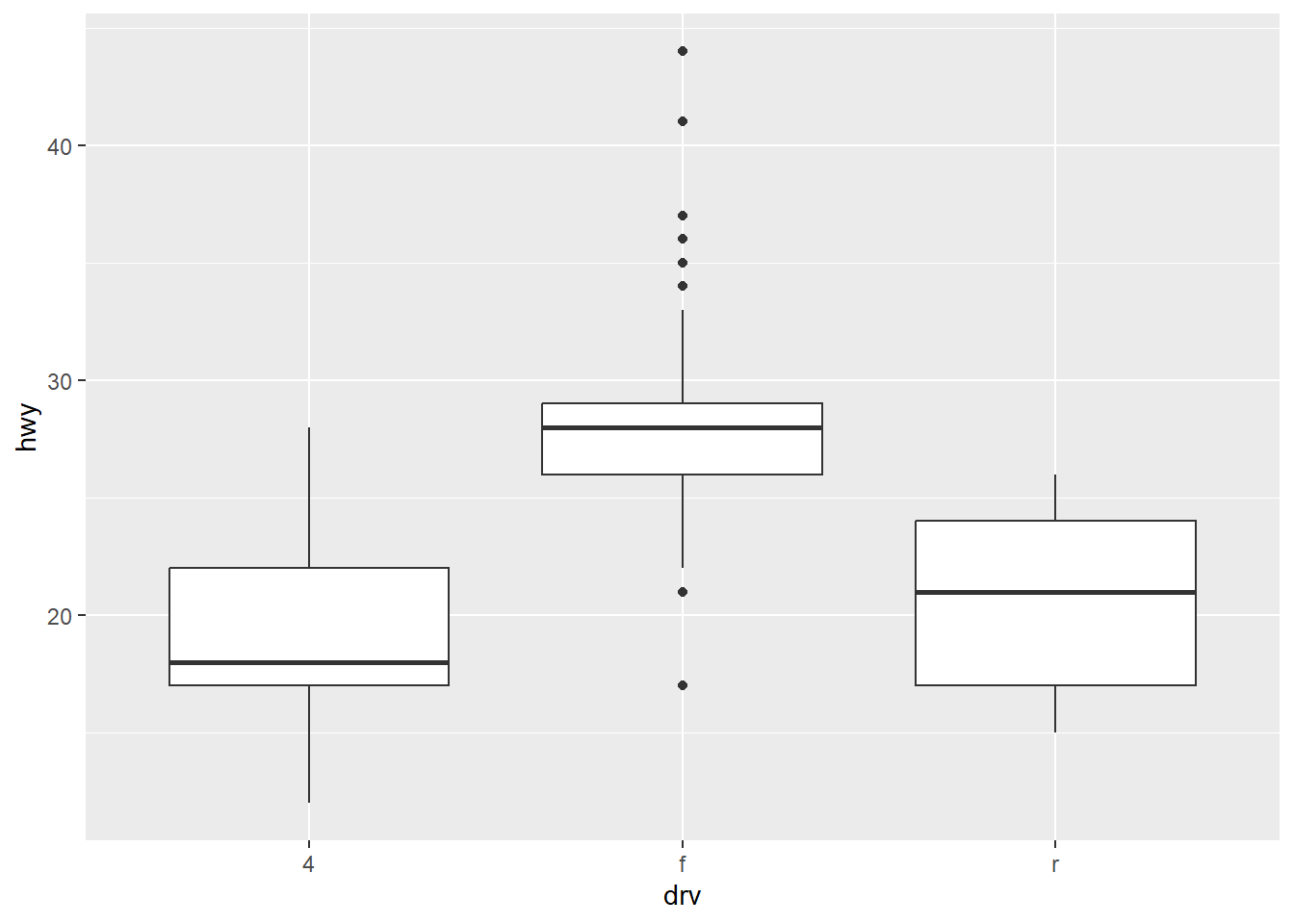
均值线与误差棒图

以ToothGrowth 数据集为例，先自定义分组汇总函数计算分组均值和标准误：

my_summary <- function(data, .summary_var, ...) {
  summary_var <- enquo(.summary_var)
  data %>%
    group_by(...) %>%
    summarise(
      mean = mean(!!summary_var, na.rm = TRUE),
      sd = sd(!!summary_var, na.rm = TRUE)
    ) %>%
    mutate(se = sd / sqrt(n()))
}
df <- my_summary(ToothGrowth, len, supp, dose)
df

## # A tibble: 6 × 5
## # Groups:   supp [2]
##   supp   dose  mean    sd    se
##   <fct> <dbl> <dbl> <dbl> <dbl>
## 1 OJ      0.5 13.2   4.46  2.57
## 2 OJ      1   22.7   3.91  2.26
## 3 OJ      2   26.1   2.66  1.53
## 4 VC      0.5  7.98  2.75  1.59
## 5 VC      1   16.8   2.52  1.45
## 6 VC      2   26.1   4.80  2.77

pd <- position_dodge((0.05))
ggplot(df, aes(dose, mean, color = supp, group = supp)) +
  geom_errorbar(aes(ymin = mean - se, ymax = mean + se),
    color = "black", width = 0.1, position = pd
  ) +
  geom_line(position = pd) +
  geom_point(position = pd, size = 3, shape = 21, fill = "white") +
  xlab(" 剂量(mg)") +
  ylab(" 牙齿生长") +
  scale_color_hue(
    name = " 喂养类型", breaks = c("OJ", "VC"),
    labels = c(" 橘子汁", " 维生素C"), l = 40
  ) +
  scale_y_continuous(breaks = 0:20 * 5)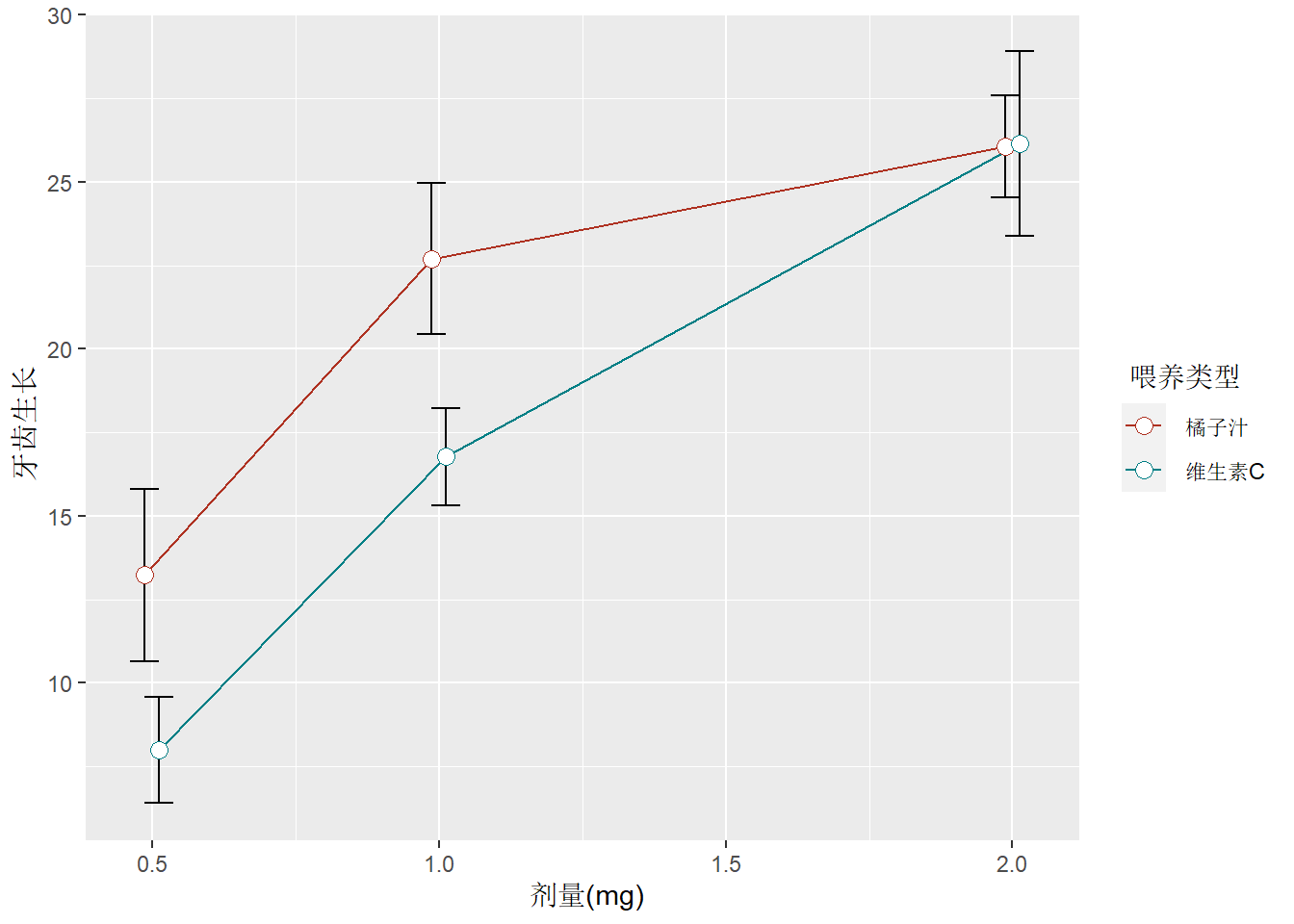

5.3.3 列联表

对分类变量做描述统计，通常是计算各水平值出现的频数和占比，得到列联表（交叉表）。用table() 可以实现，但功能很弱还不够tidy. janitor 包提供了更强大的tabyl() 函数，可以生成一个、两个、三个变量的列联表，再结合adorn_*() 函数，可以很方便地按想要的格式添加行列合计、占比等。

一维列联表，添加合计行：

library(janitor)

## Warning: package 'janitor' was built under R version 4.2.3

## 
## Attaching package: 'janitor'

## The following object is masked from 'package:rstatix':
## 
##     make_clean_names

## The following objects are masked from 'package:stats':
## 
##     chisq.test, fisher.test

mpg %>%
  tabyl(drv) %>%
  adorn_totals("row") %>% # 添加合计行
  adorn_pct_formatting() # 设置百分比格式

##    drv   n percent
##      4 103   44.0%
##      f 106   45.3%
##      r  25   10.7%
##  Total 234  100.0%

二维列联表，添加列占比和频数

library(janitor)
mpg %>%
  tabyl(drv, cyl) %>%
  adorn_percentages("col") %>% # 添加列占比
  adorn_pct_formatting(digits = 2) %>% # 设置百分比格式
  adorn_ns() # 添加频数

##  drv           4           5           6           8
##    4 28.40% (23)   0.00% (0) 40.51% (32) 68.57% (48)
##    f 71.60% (58) 100.00% (4) 54.43% (43)  1.43%  (1)
##    r  0.00%  (0)   0.00% (0)  5.06%  (4) 30.00% (21)